How to interpolate values with Accelerate framework in Swift

I recently had to research methods to draw curves through a set of points. While interpolation wasn’t the most appropriate and efficient approach in my case, I still had some fun with the Accelerate framework (which optimizes large-scale mathematical computations).

1. What is an interpolation?

In the mathematical field of numerical analysis, interpolation is a type of estimation, a method of constructing new data points within the range of a discrete set of known data points. (Sheppard, William Fleetwood)

For instance, let’s say you’re eating delicious pasta. Your plate contains 20 gnocchi, and you eat them continuously in a 10 min period of time. While the scenario can be managed by head ([0, 2, 4, …, 18, 20]), it’s a task that interpolation algorithms can easily achieve, whatever the numbers.

2. Examples to interpolate using Accelerate framework

Besides implementing the logic in simple Swift code, you can directly use the Accelerate framework which should fasten the process!

2.1 Simple interpolation (Gnocchi)

So let’s say we want to interpolate how the 20 gnocchi are eaten within the 10 minutes timeframe, we could write:

1
2
3
4

let gnocchiValues: [Double] = [0, 20]
let timeIndices: [Double] = [0, 10]

let result = vDSP.linearInterpolate(values: gnocchiValues, atIndices: timeIndices)

The output should be [0.0, 2.0, 4.0, 6.0, 8.0, 10.0, 12.0, 14.0, 16.0, 18.0, 20.0], meaning that at minute 2, 4 gnocchi should be gone.

More information about this “basic” linear interpolation in the documentation.

2.2 Complex interpolation (CGPoint)

The previous code works fine with values that follow on another (e.g. [1, 2, 3]). But what about more complex inputs as set of CGPoints where y axis values go up and down? (e.g. [(x: 1, y: 1.5), (x: 2, y: 5.0), (x: 3, y: 3.5)]).

We could directly dive into a CGPoint example, but we’ll cover this part in the next section. For now, let’s focus on the “y” value which requires interpolation (in the case your curve is horizontal).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

let steps = vDSP_Length(100) // (1)
let stride = vDSP_Stride(1) // (2)
let values: [Float] = [1, 5, 2, 15, 20, 10, 9, 8, 15, 20] // (3)

let denominator = Float(steps) / Float(values.count - 1)
let control: [Float] = (0..<steps).map { // (4)
    let x = Float($0) / denominator
    return floor(x) + simd_smoothstep(0, 1, simd_fract(x))
}

var result = [Float](repeating: 0, count: Int(steps)) // (5)
vDSP_vlint(values, control, stride, &result, stride, steps, vDSP_Length(values.count))

1. steps is the length of the output (number of interpolation points).
2. stride holds differences between indices of elements (our x axis for CGPoint).
3. values holds the y value of our CGPoints (as it’ll be an horizontal alignment).
4. control holds the fractional part to interpolate between the values.
5. result holds the output of the linear interpolation.

It may seem a bit harsh at first gland. I highly suggest reading the official documentation about linear interpolation functions. Note it exists for quadratic interpolation functions too.

3. CGPoint extension for linear interpolation

Our input vector isn’t compatible with CGPoints: we have to take care of the intermediate logic ourselves.
If you want to directly read the extension code, check this file.

Let’s create a CGPoint extension:

• Depending on the graph direction, we should use either x or y axis.
• The number of interpolated points should be dynamic.
• And let’s allow a switch between linear and quadratic interpolation.

There are two additional steps compared to the previous code:

1. Extract the “values” from the CGPoint list.
2. Construct the new CGPoint list based on the interpolation output.

Let’s put our extension inside a new file called CGPoint+Interpolation.

1
2
3
4
5
6
7

import CoreGraphics.CGGeometry
import Accelerate.vecLib
import simd

extension Array where Element == CGPoint {
	
}

As mentionned above, we plan to a/ handle both horizontal and vertical cases, and b/ handle the linear and quadratic interpolations. For this purpose, let’s create two ENUMs:

1
2
3
4
5
6
7

enum InterpolationAxis: CaseIterable {
    case horizontal, vertical
}

enum InterpolationAlgorithm: CaseIterable {
    case linear, quadratic
}

Let’s keep the extension method simple:

1
2
3
4
5
6

func interpolated(direction: InterpolationAxis = .horizontal, 
		algorithm: InterpolationAlgorithm = .linear, 
		steps: Int = 1024) -> [CGPoint]
{
	
}

Extracting the input vector from our CGPoint list isn’t difficult.

1

let values: [Float] = isHorizontal ? self.map({ Float($0.y) }) : self.map({ Float($0.x) })

However, constructing the output requires more lines as we add data instead of removing some.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

let pointMinimum: CGFloat = (isHorizontal ? self.first?.x : self.first?.y) ?? 0
let pointMaximum: CGFloat = (isHorizontal ? self.last?.x : self.last?.y) ?? 0
let pointStep: CGFloat = (pointMaximum - pointMinimum) / CGFloat(steps - 1)
if isHorizontal == true {
    return result.enumerated().map { (index, value) -> CGPoint in
        CGPoint(
            x: pointMinimum + (CGFloat(index) * pointStep),
            y: CGFloat(value)
        )
    }
} else {
    return result.enumerated().map { (index, value) -> CGPoint in
        CGPoint(
            x: CGFloat(value),
            y: pointMinimum + (CGFloat(index) * pointStep)
        )
    }
}

Then you merge this with the logic we wrote a bit earlier, and voilà.

You can read the full code in the GitHub project, and specifically here.

4. Wrapping the fun inside a SwiftUI project

I spent some time having fun with SwiftUI. You can download the Xcode project and play with it. Check the animation below as a small demo.

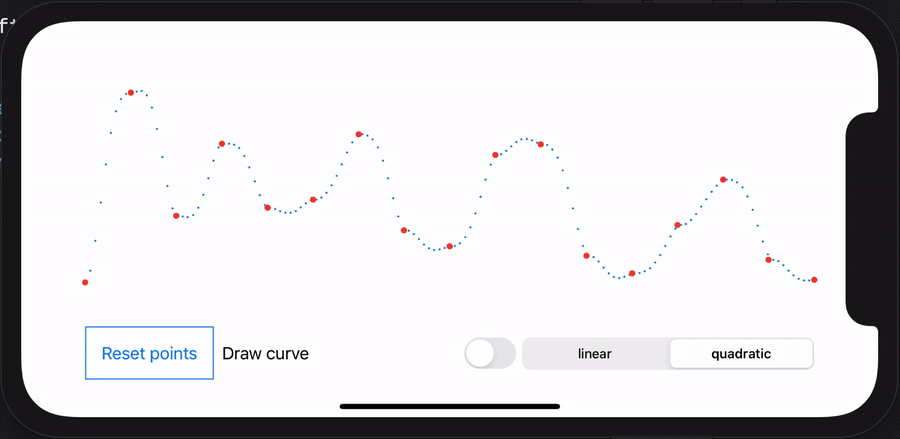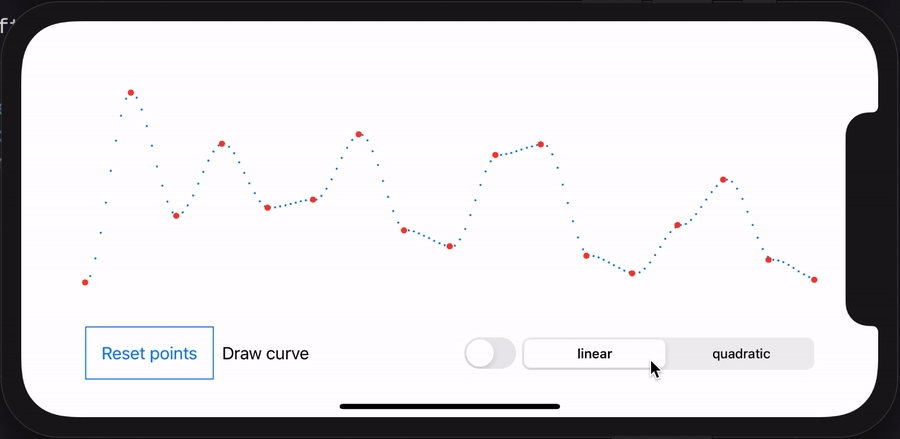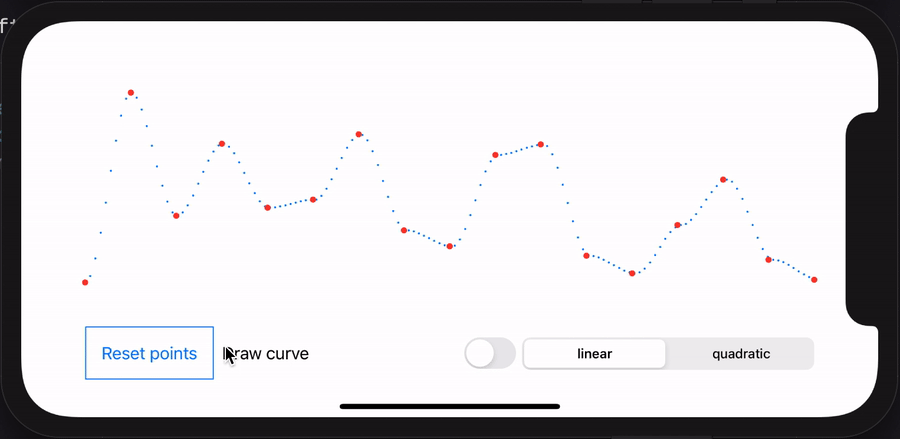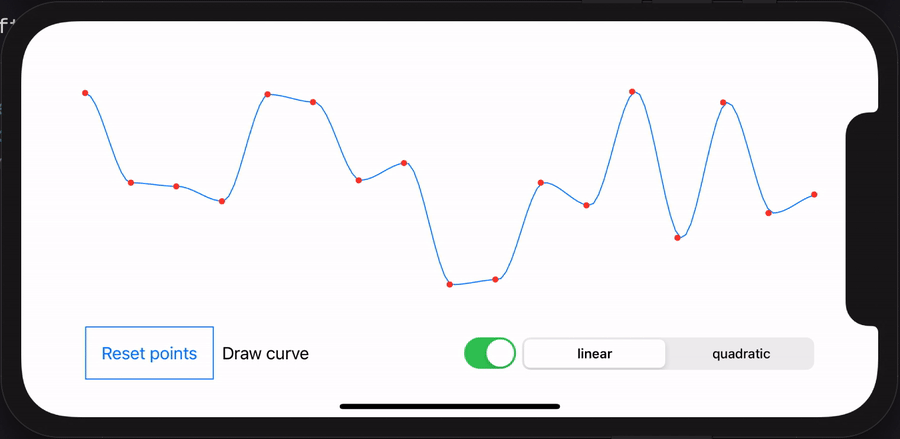
• The red points are randomly generated.
• The blue points are generated from the interpolation.
• The blue line is drawn from the interpolation points.
• You can switch between linear and quadratic algorithm.

Special thanks to Axel Le Pennec for mentioning the interpolation (Accelerate) methods to me.